什么是并查集?
一句话解释并查集的作用:快速找到元素所属集合
并查集主要涉及两种操作:合并(union)、查找(find)
- 合并(union):将两个不同集合合并为一个集合
- 查找(find):查找元素的父节点
为了便于理解并查集,先来看一道题:连通网络的操作次数(leetcode 1319)
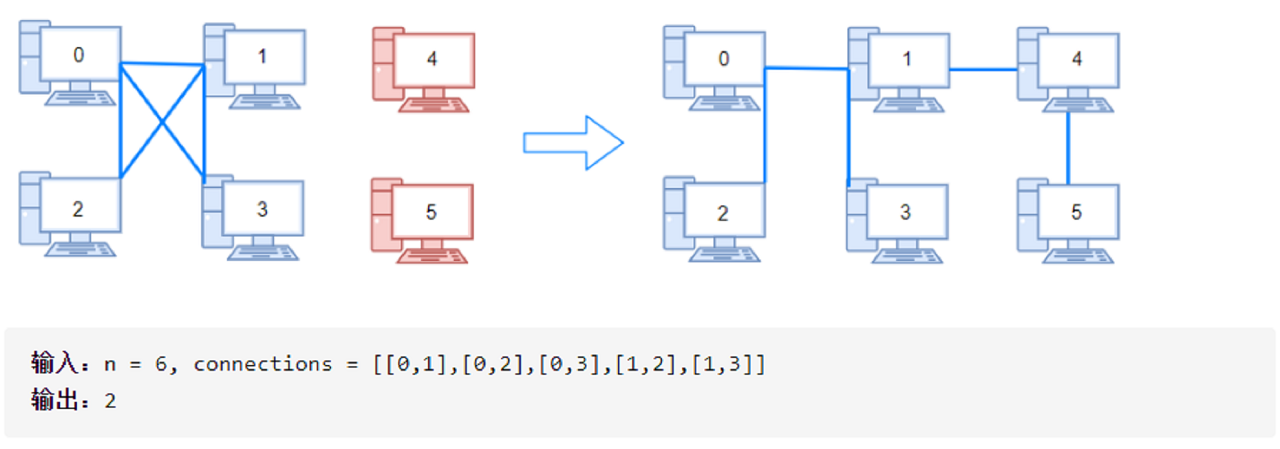
用以太网线缆将 n 台计算机连接成一个网络,计算机的编号从 0 到 n-1。线缆用 connections 表示,其中 connections[i] = [a, b] 连接了计算机 a 和 b。 网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。 给你这个计算机网络的初始布线 connections,你可以拔开任意两台直连计算机之间的线缆,并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能,则返回 -1 。
leetcode 1319. 连通网络的操作次数
1.初始化并查集
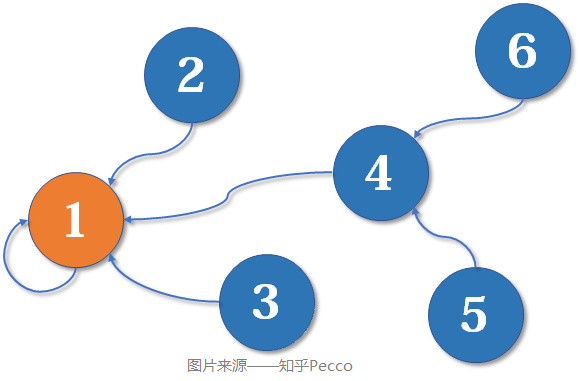
并查集的初始阶段,所有元素都是独立的节点,也就是各成一派,各节点的父节点为自己本身
def __init__(self, n):
#整个集合中共有多少节点
self.n = n
#表示每个子集分别有多少个节点
self.rank = [1] * n
#初始阶段每个元素为独立的节点,父节点为自己本身
#例如上题的计算机编号从0到n-1,意味着计算机可以用0到n-1的数字分别表示
self.father = list(range(n))2.根据问题进行合并(union)
连接网络的操作次数这道题初始阶段分为两部分,一部分是已经连接好的计算机,另一部分是等待连接的计算机,那么接下来需要将题目给出的connections数组中的计算机合并(union)
def union(self, x: int, y: int) -> bool:
#首先需要找到合并的计算机的根节点
fx, fy = self.find(x), self.find(y)
#如果他们根节点相同,意味着他们属于一个集合,则不需要合并
if fx == fy:
return False
#为了避免发生节点串联的情况,将节点数较少的子集合并到节点数较多的子集
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
#合并,将fy(子集数较少的根节点)的父节点指向fx
self.father[fy] = fx
return True我们可以看到合并的开始使用了查找(find)的操作,也就是判断合并的节点是否属于同一个子集
def find(self, x: int) -> int:
#如果父节点是自己本身则返回
#值得一提的是只有根节点的父节点是自己,而初始时所有的节点都是根节点
if self.father[x] == x:
return x
#路径压缩,例如3的父节点是2,2的父节点是1,压缩后3和2的父节点均为1
self.father[x] = self.find(self.father[x])
return self.father[x]3.针对不同的问题进行分析
并查集的主要框架和模板已经有了,现在就要根据不同的问题进行分析。
如连接网络的操作次数这题,我们需要计算多余的线缆,分析可以得到,在初始化阶段,多余的线缆与合并两台计算机时发现他们 根节点相同 是等价的,因此可以增加辅助变量 extra_num 记录发生根节点相同时的次数。
我们同样还需要计算有多少台计算机需要线缆连上,值得一提的是这里所说的需要连接的计算机,可能不只是一台计算机需要连接,而是一组计算机需要连接,因此这与并查集中 子集数-1 是等价的,因此增加 left_num 记录子集数
完整代码如下:
class UnionSet:
def __init__(self, n):
self.n = n
self.rank = [1] * n
self.father = list(range(n))
self.left_num = n
self.extra_num = 0
def find(self, x: int) -> int:
if self.father[x] == x:
return x
self.father[x] = self.find(self.father[x])
return self.father[x]
def union(self, x: int, y: int) -> bool:
fx, fy = self.find(x), self.find(y)
if fx == fy:
self.extra_num += 1
#多余线缆+1
return False
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
self.father[fy] = fx
self.left_num -= 1
#合并成功,子集数-1
return True
class Solution:
def makeConnected(self, n: int, connections: List[List[int]]) -> int:
union_set = UnionSet(n)
for connect in connections:
union_set.union(connect[0], connect[1])
#如果线缆数小于子集数-1意味着无法满足题目条件,返回-1
return union_set.left_num - 1 if union_set.left_num - 1 <= union_set.extra_num else -1并查集怎么用
还有类似上述题目形式的题,例如959.由斜杠划分区域,此题稍有不同的地方在于每一个节点是二维的,也就是(x, y)的形式,但稍作转换,如将10x+y表示一个节点就能将二维的转换为一维的,也就可以直接套模板了。
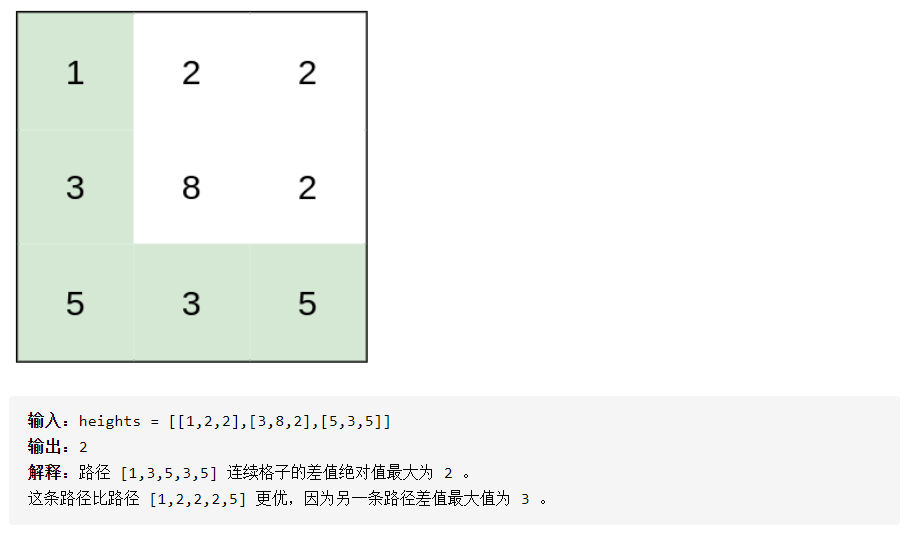
但这些题有些过于契合并查集了,而有些题往往不会给出直观的表达,例如1631. 最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。 一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。 请你返回从左上角走到右下角的最小 体力消耗值 。
这种类型的题需要有一定的抽象能力,将其抽象成图的形式,再找到并查集能套用的点,详情可参考负雪明烛大佬的解析。通常情况下并查集可以作为点与点之间关系的突破口,当然也有更特殊的情况721. 账户合并,字符串的转换需要进一步的对并查集有更深的理解,否则可能一杯茶,一包烟,一道leetcode做一天
以下列出一些并查集相关的题目,温故而知新:
二维点相关:
图相关:
字符串相关:
参考链接:知乎用户@Pecco






Can I simply say what a comfort to find someone that actually understands what theyre discussing on the net. You actually realize how to bring a problem to light and make it important. More and more people really need to read this and understand this side of your story. I was surprised that youre not more popular since you definitely possess the gift.
I was very happy to discover this site. I wanted to thank you for ones time just for this fantastic read!! I definitely really liked every bit of it and i also have you saved as a favorite to see new things on your site.
Itís hard to come by knowledgeable people for this subject, but you sound like you know what youíre talking about! Thanks
Can I simply say what a aid to search out somebody who truly knows what theyre talking about on the internet. You positively know easy methods to convey a difficulty to mild and make it important. More individuals must learn this and understand this side of the story. I cant consider youre not more fashionable because you definitely have the gift.
I have been surfing on-line greater than 3 hours nowadays, but I by no means discovered any interesting article like yours. It is lovely value sufficient for me. Personally, if all web owners and bloggers made good content material as you probably did, the internet can be a lot more helpful than ever before.
I’m still learning from you, but I’m making my way to the top as well. I certainly love reading all that is written on your site.Keep the aarticles coming. I loved it!
F*ckin¦ amazing things here. I am very happy to peer your article. Thank you a lot and i am taking a look forward to contact you. Will you please drop me a mail?
Sure, you can contact me by 649339335@qq.com
I actually wanted to construct a small remark to thank you for those unique solutions you are giving on this site. My extensive internet look up has finally been paid with excellent facts and techniques to go over with my good friends. I ‘d admit that many of us readers actually are rather fortunate to dwell in a magnificent place with very many awesome individuals with very helpful hints. I feel truly privileged to have come across your web pages and look forward to many more amazing moments reading here. Thanks once more for everything.
What i do not understood is in fact how you are now not really a lot more smartly-liked than you may be now. You are so intelligent. You already know therefore significantly relating to this subject, made me in my view believe it from numerous numerous angles. Its like women and men don’t seem to be interested unless it is one thing to accomplish with Girl gaga! Your personal stuffs great. At all times handle it up!
Great write-up, I am normal visitor of one’s site, maintain up the excellent operate, and It is going to be a regular visitor for a long time.